Fixed and variable costs

Possibly of even greater importance than the distinction between capital costs and operating costs is the distinction between fixed costs and variable costs. You will see that the main argument for the cost-efficiency of ODL - the expectation that distance learning generates economies of scale - rests on this distinction.

The distinction relates to volume of activity. The principal activities of an ODL institution consists in teaching students. Hence fixed costs are those which do not increase with the volume of activity, i.e. the number of students taught. Development costs of teaching materials are fixed costs in this sense. You need only develop the study guides once for a particular course and they can be used by many learners. Of course, you would have to reprint them as new students enroll but the development costs remain a one-off. The costs for reprinting and posting the materials to the students are examples of variable costs. Ideally, all costs can be classified as either fixed or variable. However, some costs are classified as semi-variable. These are costs, which are fixed up to a certain threshold. Typical semi-variable costs are costs of class tutors.

	Activity A8: Classifying cost-drivers as fixed or variable costs
1. Open the spreadsheet Activity A08. 2. Classify each cost driver in the list as follows: select an item from the list copy and paste it onto the stars of one of the categories the evaluation will tell you whether you have correctly categorized the item. Click here

Note well that the VxN for Variable costs is a composed term in which V stands for Variable cost per student and N for Number of students. (Example: if it costs US$ 4 per student to replicate some content on a CD-ROM and post it to the respective student, it costs US$ 400 to do the same for all hundred students you may have in the same course. The respective Variable costs come to US$ 400, or US$ 4 per student times 100, the number of students.)

The Total Costs equation is a function of N (total costs depending on the number of students). In order to denote this mathematicians would write: TC(N) = F + VxN.

Activity A9: Exploring the Total Costs equation

This activity allows you to vary the fixed and variable parts of the cost equation so that you can see how the graph of the costs varies. 1. Open the Excel spreadsheet A09. 2. Try changing the variable costs per student. What happens? 3. Try changing the fixed costs. What happens? (If you want to understand the maths behind this, you may recall that the equation   TC(N) = F + V × N is a linear equation of the form f(x) = kx + c where c is the intersection with the y-axis and k is the gradient (slope) of the graph. In our case the constant is F which identifies the starting plateau of the costs, while V (variable cost per student) is the gradient. The higher the value of V, the steeper the gradient.) Click here

It is important to understand this equation clearly, because it provides important guidelines for cost-efficient course planning. The important point is what happens to average costs as N increases.

As N increases, AC decreases, other things being equal.

This is what is meant by economies of scale.

The right-hand side of the equation is made up of two components. The first, F/N decreases as N increases. The second, V, does not change as N increases since it is the variable cost per student.

This result is often described as the fixed costs are 'spread over more students'. Each student is charged a part of the fixed costs. The more students there are, the less each has to pay.

This is what educational planners want: falling unit costs. Mathematicians like to look at extremes and ask what would happen if we were to increase the number of students ad infinitum. The answer is that, in this case, the first term (F/N) approaches zero or, in mathematical language, the average costs 'converge to' V.

Activity A10: Exploring the Average Costs equation

The average costs graph (Figure 1) shows how cost-effectiveness arises from increasing student numbers. 1. Open the spreadsheet Activity A10. 2. Try different values of F and V to see how the graph changes. Note on the maths The AC equation is an algebraic transformation of the total cost equation (TC). You can see from the graph that the line is asymptotic - that is, it tends towards the long-term value V but never quite reaches it. AC is only defined for N> = 1. AC(1) = F + V. Since often V is almost negligible, AC(1) is approximately F while AC(N) for very big N is approximately V. This differential between F and V identifies the scope for any economies of scale. Click here

Figure 1: Average costs and economies of scale

It is important to note that AC cannot fall below V, however large the number of students becomes. The variable costs per student therefore represent a bottom line, below which the average costs per student cannot fall. This implies an important strategic guideline:

To lower average costs per student keep variable cost per student low.

The other strategic guideline has already been mentioned:

To bring the average cost per student down, increase the number of students.

This guideline needs some additional comment. The cube in Figure 2 shows that economies of scale vary according to the number of students already enrolled. The higher the number of students, the lower the average costs reduction effect of including another student. Hence you have to judge whether it makes sense to increase student numbers when economies of scale are already largely exhausted.

Of course, the number of students cannot be increased at will. You need to attract students and marketing efforts themselves are a cost factor and may not succeed in increasing numbers at an economic cost. Students may prefer multi-media courses with high level of learner support. If you want to offer this in order to attract further students you will need to increase V or F or both. Hence, it is important to keep in mind that N, F, V are not independent. The behavior of N is influenced by V and F. If you lower one of these parameters, students may walk away from your course and the plan to lower average costs may backfire, because the lower number of students means that fixed costs can be spread only over fewer numbers such that average cost per student will rise, possibly initiating a vicious circle.

Perraton's Costing Cube

Perraton (2000, p.137) has portrayed the relation between volume, media sophistication and the interactivity. His cube (Figure 2) has three dimensions and the arrows show the direction of reducing cost per student.

Figure 2: Perraton's Costing Cube


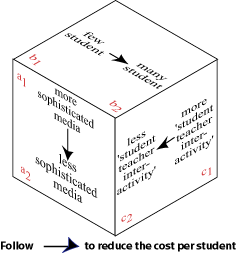
In fact, Perraton's visualization is very close to the average cost formula. The fixed costs in distance education are generally related to media sophistication, the variable cost per student is strongly influenced by the level of interactivity. (The cube is slightly modified. The original cube speaks only about face-to-face tuition. However, meanwhile we can sustain teacher student interaction at a distance (e.g. videoconferencing, online conferencing). But all these forms of interactivity between students and teacher, irrespective of the technology used, claim the teacher's time and increase variable costs. ) The Internet and videoconferencing influence the cost per student as much as face-to-face tuition does. The number of students, varying from few to many, is explicitly referred to in both models.


Marginal costs

We need to include a definition of marginal costs since the term is part of the language of ODL.

Strictly speaking marginal cost means the cost of including one more student in your system.

We can express this like this in mathematical language:


MC = TC (N + 1 )- TC (N) = [FC + V x (N + 1)] - [FC + V x N] = FC - FC + V x (N + 1) - V x N = V

Where MC: Marginal Costs

The equation shows that the cost of including one more student in your system is equal to the variable cost per student. The interesting point here is that fixed costs do not impact on marginal costs. Offering something at marginal costs therefore strictly speaking means to offer it at a price that makes no contribution to fixed costs.

Fixed costs in ODL are mainly related to development costs. Saying you offer something at marginal costs often implies that you are willing to write-off the development costs.


Semivariable costs

We have treated fixed costs and variable costs so far as a binary distinction. This means any cost driver can either be treated as fixed cost or as variable cost per student, as F or as V. This is a little unrealistic. In practice, many costs are semivariable Such costs are fixed up to a certain threshold volume.

For example, you can increase the number of students in an online seminar without adding another class as long as the number of students is below the maximum class size. Beyond this size you need to start a new class and employ an additional tutor.

The graph of a semi-variable cost takes the form of a step function: within limits you may increase volume of activity (i.e. number of students) without raising costs. At a certain point costs will jump.

Formally, we define semivariable cost function as follows:

SV = [N/G] x SN

Note that the number of groups (or classes) needed is defined by the number of students in the system and the maximum group size.

Theoretically, it can be argued that all costs are semi-variable Most cost drivers are to some extent affected by an increase in the volume of activity if only the increase is big enough. It may be that the concept of sem-ivariable costs has been ignored in ODL for so long because ODL was largely seen as 'individual studies'. Nowadays it is increasingly possible to teach classes at a distance. In this case the notion of semi-variable cost as distinct from fixed and variable costs per student becomes more and more important.

Total Costs = Fixed costs + Semivariable costs + Variable costs

TC = F + [N/G] x SN + V x N

Activity A11: Exploring the effects of group size (TC)

This activity explores semivariable costs. 1. Use spreadsheet Activity A11 for this. 2. Try changing the group size. 3. Then try different combinations of fixed cost, variable cost, semivariable cost and group size. 4. Observe what happens in each case. In ODL systems with little or no group work, semivariable costs are not very important and can usually be ignored. When there is a significant amount of group work, semivariable costs become important. You can see why as you change the input values in this spreadsheet. Click here

This leads to a modification of average costs also:

AC = TC/N

AC = F/N + ([N/G] x SN) / N + (VxN)/N

AC = F/N + SN/G + V

	Activity A12: Exploring the effects of group size (AC)
This activity looks at the effect of group size on the average cost equation. 1. Use the spreadsheet Activity 12 for this. 2. Try different group sizes to see their effect on average cost. The effects of group size on the graph are generally less visible. Click here

Unit costs

Another useful concept is unit costs. You have seen that various cost drivers can be seen as variable cost per student, e.g.:

print costs per student

postage costs per student.

In order to keep unit costs low you need to control all the items that contribute to unit cost per student.

The main lessonthat we can draw from our study of semi-variable costs is that larger group sizes lead to greater cost efficiency. The drawback is that this reduces the level of interactivity, a feature, which many see as an important indicator of quality.

The generic costing template and the fixed costs/variable costs distinction

How does the generic costing template relate to the distinction between fixed and variable costs? Table 8 below classifies some cost drivers.

Summary and caveat:

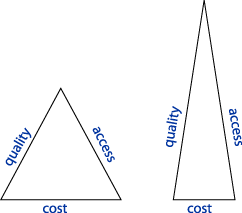
John Daniel portrays these expectations by his eternal triangles as in Figure 3. According to Daniel (2001) the cost structure of ODL allows costs to be reduced while at the same time increasing access and quality. This reflects our theoretical expectations, but it makes assumptions that may not apply in every context.

Figure 3: The cost-quality-access triangle